Analoga integratorer: Hur man använder dem för sensorgränssnitt, signalgenerering och filtrering

Innan elektronikvärlden blev digital, använde styrsystem som byggde på lösningen av differentiella ekvationer, analog beräkning för att lösa dessa ekvationer. Som en följd av detta var analoga datorer ganska vanliga eftersom nästan alla lösningar på differentialekvationer kräver förmåga att integrera signaler. Även om styrsystem mestadels har blivit digitala och numerisk integration har ersatt den analoga integrationen, finns det fortfarande ett behov av analoga integratorkretsar för drift av sensorer, signalgenerering och filtrering. Dessa tillämpningar använder integratorer baserade på operationsförstärkare (engelska "op amps") med kapacitiva element i återkopplingsslingan för att åstadkomma önskad signalbehandling i lågeffekttillämpningar.

Även om det fortfarande är viktigt, kan många konstruktörer lätt förbise hur användbara de är. Denna artikel ger en översikt över integratorkretsar och vägledning om korrekt konstruktion, val av komponenter och de bästa metoderna för att uppnå en utmärkt prestanda med hjälp av flera exempel från Texas instrument .

Grundläggande inverteringsintegrator

Den klassiska analoga integratorn använder en operationsförstärkare med en kondensator som ett återkopplingselement (figur 1).

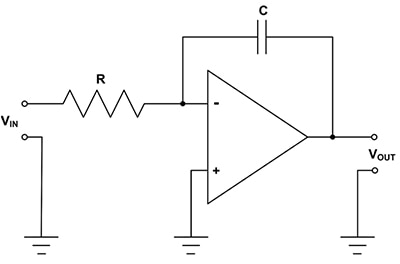Figur 1: Den grundläggande inverterande analoga integratorn består av en operationsförstärkare med en kondensator i återkopplingsslingan. (Bildkälla: DigiKey)

Utgångsspänningen, V _UT från integratorn som en funktion av insignalen, V _I, kan beräknas med ekvation 1.

Ekvation 1

Förstärkningsfaktorn för den grundläggande inverteringsintegratorn är -1/RC applicerat på ingångsspänningens integral. I praktiken bör kondensatorer som används för integratorer ha snävare toleranser än 5 % och låg temperaturavdrift. Polyesterkondensatorer är ett bra val. Motstånd med ± 0,1 % tolerans bör användas i kritiska punkter i kretsen.

Det finns en begränsning i denna krets då kondensatorn vid likström (DC) utgör en öppen krets och förstärkningen går mot oändligheten. I en praktisk krets skulle utgången då slå i taket, och gå till antingen den positiva eller negativa matningsnivån, beroende på polariteten hos den icke-nollade DC-ingången. Detta kan korrigeras genom att begränsa integratorns DC-förstärkning (figur 2).

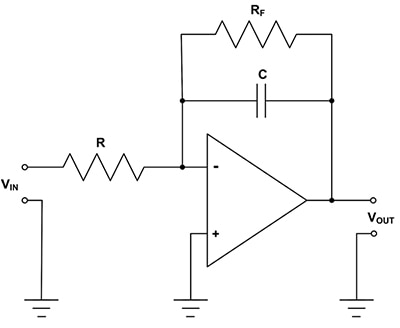Figur 2: Att lägga till ett stort motstånd parallellt med återkopplingskondensatorn begränsar DC-förstärkningen och resulterar i en praktisk integrator. (Bildkälla: DigiKey)

Om ett högvärdesmotstånd (R _F) läggs till parallellt med återkopplingskondensatorn begränsas DC-förstärkningen för basintegratorn till värdet på -R _F / R, vilket resulterar i en praktiskt användbar komponent. Detta tillägg löser DC-förstärkningsfrågan men begränsar frekvensområdet som integratorn fungerar över. Att titta på en verklig krets hjälper dig att förstå denna begränsning (figur 3).

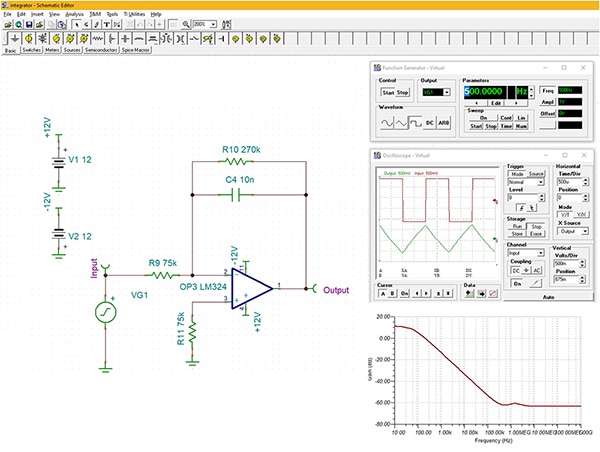Bild 3: En TINA-TI-simulering av en praktisk integrator med verkliga komponenter. (Bildkälla: DigiKey)

Denna krets använder en LM324-operationsförstärkare från Texas Instruments. LM324 är en bra generell operationsförstärkare med låg ingångsförspänningsström (45 nA typiskt), låg offsetspänning (2 mV typiskt) och en produkt av förstärkning x bandbredd på 1,2 MHz). Kretsingången drivs av simulatorns funktionsgenerator med en fyrkantvåg på 500 Hz. Detta visas som den övre grafen på simulatorns oscilloskop. Kretsen integrerar kvadratvågen och utgången blir en trekantfunktion på 500 Hz som visas som det nedre oscilloskopspåret.

DC-förstärkningen är -270 kΩ / 75 kΩ eller -3,6 eller 11 dB; detta ses i överföringsfunktionen för kretsen, som visas i det nedre högra rutnätet i figur 3. Frekvenssvaret avtar med -20 dB per dekad från cirka 100 Hz till cirka 250 kHz. Detta är det användbara frekvensområdet för integratordrift och det är relaterat till förstärkarens produkt av förstärkning x bandbredd.

En nyare operationsförstärkare är Texas Instruments TLV9002 . Denna förstärkare med 1 MHz förstärkning x bandbredd har en ingångsoffsetspänning på ± 0,4 mV och en extremt låg förspänningsström på 5 pA. Som en CMOS-förstärkare är den avsedd för en mängd bärbara tillämpningar till låg kostnad.

Det är viktigt för konstruktörer att komma ihåg att en integrator är en kumulativ komponent. Som sådan och utan lämplig kompensation kan ingångsförspänningsströmmen och ingångsoffsetströmmen resultera i att kondensatorspänningen ökar eller minskar över tiden. I denna tillämpning är förspänningsströmmen på ingången och offsetspänningen relativt låg, och ingångsspänningen tvingar återkopplingskondensatorn att urladdas med jämna mellanrum.

I tillämpningar som använder ackumuleringsfunktionaliteten måste det, som vid mätning av laddning, finnas en mekanism för att återställa spänningen och återställa de initiala förhållandena i integratorn. Texas Instruments ACF2101BU har en sådan mekanism. Det är en dubbelswitchad integrator som innehåller en inbyggd switch för att ladda ur återkopplingskondensatorn. Eftersom enheten är avsedd för tillämpningar som kräver laddningsackumulering, har den en extremt låg förspänningsström på 100 fA och en typisk offsetspänning på ± 0,5 mV.

En liknande switchad integrator/transimpedansförstärkare är Texas Instruments IVC102U . Den är avsedd för samma tillämpningsområde som ACF2101BU:an men skiljer sig åt i att det bara är en produkt per kapsling. Den har också tre interna återkopplingskondensatorer. Den innehåller switchar för att ladda ur kondensatorbanken och ansluta ingångskällan, så att konstruktören får möjlighet att styra integrationsperioden och inkludera en hållfunktion samt att ladda ur spänningen på kondensatorn.

Icke-inverterande integrator

Den grundläggande integratorn inverterar signalens integral. Medan en andra inverterande operationsförstärkare som är ansluten i serie med basintegratorn kan återställa den ursprungliga fasen, är det möjligt att konstrukera en icke-inverterande integrator i ett enda steg (figur 4).

Figur 4: En icke-inverterande integrator baserad på en operationsförstärkarkonfiguration med differensförstärkning säkerställer att utgångsfasen matchar ingångsfasen. (Bildkälla: DigiKey)

Den icke-inverterande versionen av integratorn använder en differensintegrator för att hålla utgången i fas med insignalen. Denna konstruktion lägger till ytterligare passiva komponenter, vilka bör matchas för optimal prestanda. Förhållandet mellan ingångs- och utgångsspänningarna är detsamma som basintegratorn, med undantag för tecknet, såsom visas i ekvation 2:

Ekvation 2

Andra anpassningar till basintegratorn kan förverkligas med traditionella operationsförstärkarkretsar. Exempelvis kan ingångar med flera spänningar (V ₁, V ₂, V ₃...) läggas till genom att summera var och en genom sitt eget ingångsmotstånd (dvs. R ₁, R ₂, R ₃...) till den icke-inverterande ingången till operationsförstärkaren. Den resulterande utsignalen från denna summerande integrator beräknas med ekvation 3:

Ekvation 3

Om R ₁ = R ₂ = R ₃ = R beräknas utgången med ekvation 4:

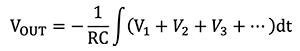Ekvation 4

Och utgången är integralen av summan av ingångarna.

Några vanliga integratortillämpningar

Historiskt har integratorer använts för att lösa differentialekvationer. Exempelvis är mekanisk acceleration förändringshastigheten, eller derivatan, av dess hastighet. Hastigheten är derivatan av förflyttningen. Integratorn kan användas på utgången från en accelerometer och integrera den en gång för att utläsa hastigheten. Om hastighetssignalen integreras blir resultatet förflyttningen. Detta innebär att genom att använda en integrator kan utgången från en enda givare producera tre distinkta signaler: acceleration, hastighet och förflyttning (figur 5).

Bild 5: Med hjälp av dubbla integratorer kan en konstruktör producera avläsningar för acceleration, hastighet och förflyttning från en accelerometer. (Bildkälla: DigiKey)

Ingången från accelerometern integreras och filtreras för att erhålla hastigheten. Hastigheten integreras och filtreras för att ge förflyttningen. Observera att alla utgångar är AC-kopplade. Detta eliminerar behovet att hantera initialvillkoren för varje integrator.

Funktionsgenerator

Funktionsgeneratorer, som matar ut flera typer av vågformer, kan konstrueras med flera integratorer (figur 6).

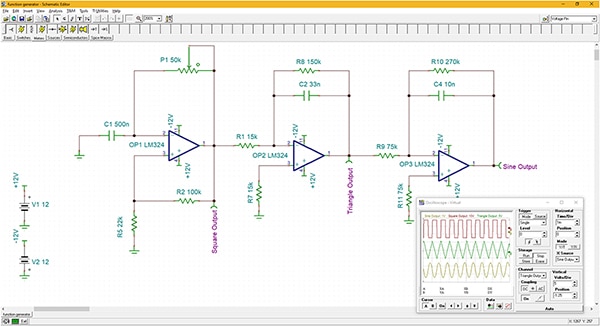Bild 6: En funktionsgenerator konstruerad med tre LM324-steg. OP1 är en relaxationsoscillator som alstrar en fyrkantvåg, OP2 är en integrator som omvandlar fyrkantvågen till en triangelvåg och OP3 är en annan integrator som fungerar som ett lågpassfilter för att ta bort de harmoniska komponenterna i triangelvågen, vilket resulterar i en sinusvåg. (Bildkälla: DigiKey)

Funktionsgeneratorn är utformad runt LM324, som omnämndes tidigare som en praktisk integrator. I denna konstruktion, visad som en TINA-TI-simulering, används tre LM324 operationsförstärkare. Den första, OP1, används som en relaxationsoscillator och producerar en fyrkantvågutgång vid en frekvens som bestäms av C1 och potentiometern P1. Det andra steget, OP2, är kopplad som en integrator och omvandlar fyrkantvågen till en triangelvåg. Det sista steget, OP3, är kopplad som integrator men är funktionellt ett lågpassfilter. Filtret tar bort alla övertoner från triangelvågen och matar ut sinusvågens grundfrekvens. Utgångarna från varje steg visas i simulatoroscilloskopet längst ner till höger i figur 6.

Rogowski-spolar

Rogowski-spolar är en klass av strömsensorer som mäter växelströmskällor med en flexibel spole som är lindad runt den strömbärande ledaren som mäts. De används för att mäta höghastighetsströmtransienter, pulserade strömmar eller 50/60 Hz nätström.

Rogowski-spolar utför en funktion som liknar en strömtransformator. Den primära skillnaden är att Rogowski-spolen använder en luftkärna i motsats till den ferromagnetiska kärnan som används i en strömtransformator. Luftkärnan har en lägre införingsimpedans, vilket resulterar i ett snabbare svar och frånvaro av mättnadseffekter vid mätning av stora strömmar. Rogowski-spolen är extremt enkel att använda (figur 7).

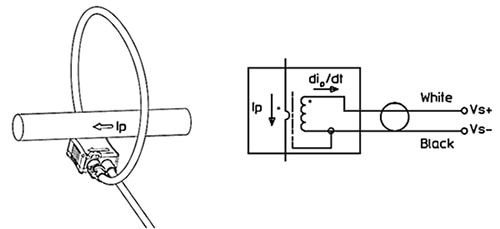Bild 7: Ett förenklat diagram som visar installationen av en Rogowski-spole runt en strömbärande ledare (vänster) och motsvarande krets för denna installation (höger). (Bildkälla: LEM USA)

En Rogowski-spole, som LEM USAART-B22-D300, är helt enkelt lindad kring den strömbärande ledaren som visas till vänster i figur 7. Den motsvarande kretsen för Rogowski-spolen visas till höger. Observera att spolens utgång är proportionell mot derivatan av den uppmätta strömmen. En integrator används för att extrahera den avkända strömmen.

En referenskonstruktion för en Rogowski-spolesintegrator visas i figur 8. Denna konstruktion har både en högprecisionsutgång som täcker ett intervall från 0,5 till 200 ampere (A) med en noggrannhet på 0,5 % och en snabb stabilisering över samma strömintervall och en noggrannhet inom 1 % på mindre än 15 ms.

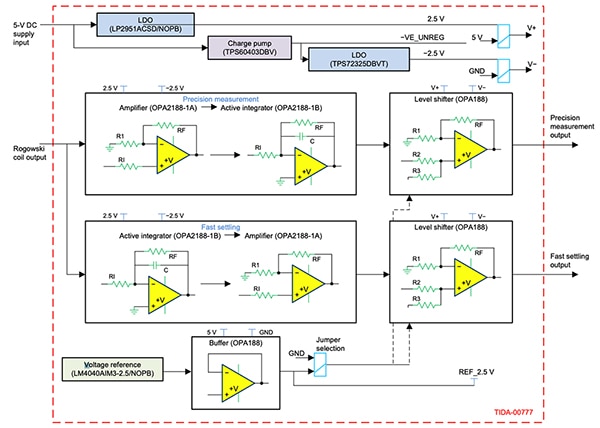Bild 8: Denna referenskonstruktion för en Rogowski-spolesintegrator använder Texas Instruments OPA2188 som den primära operationsförstärkare i integratorelementen i konstruktionen. (Bildkälla: Texas Instruments)

Referenskonstruktionen använder Texas Instruments OPA2188 som den primära operationsförstärkare i integratorelementen i konstruktionen. OPA2188 är en dubbel operationsförstärkare som använder en egenutvecklad teknik för automatisk nollställning som resulterar i en maximal offsetspänning på 25 µV och nära noll avdrift beträffande tid och temperatur. Den har en produkt av förstärkning x bandbredd på 2 MHz med en ingångsförspänningsström på typiskt ± 160 pA.

För denna referenskonstruktion valde Texas Instruments OPA2188 på grund av dess låga offset och låga avdrift av densamma. Dess låga förspänningsström minimerar också belastningen på Rogowski-spolen.

Integratorer i filter

Integratorer används i både tillståndsvariabelbaserade och bikvadratiska filterkonstruktioner. Dessa besläktade filtertyper använder dubbla integratorer för att erhålla en andra ordningens filtersvar. Tillståndsvariabelfiltret är det mer intressanta filtret, då en enda konstruktion samtidigt ger lågpass-, högpass- och bandpassvar. Filtret använder två integratorer tillsammans med ett adder-/subtraheringssteg, som visas i TINA-TI-simuleringen (figur 9). Filtersvaret för lågpassutgången visas.

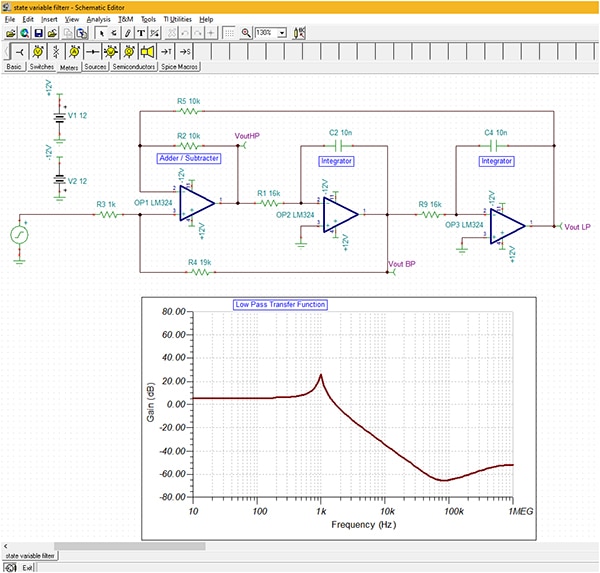Figur 9: Tillståndsvariabelfilter använder två integratorer och ett adder-/subtraheringssteg för att mata ut lågpass-, högpass- och bandpassutgångar från samma krets. (Bildkälla; DigiKey)

Denna filtertopologi har en fördel genom att alla tre filterparametrar - förstärkning, avstängningsfrekvens och Q-faktor - är justerbara oberoende av varandra i konstruktionsprocessen. I detta exempel är DC-förstärkningen 1,9 (5,6 dB), avstängningsfrekvensen 1 kHz och Q 10.

Filterkonstruktioner med högre ordning uppnås genom att placera flera tillståndsvariabelfilter i serie. Dessa filter används vanligtvis för att motverkar aliaseffekter före en A/D-omvandlare där högt dynamiskt intervall och lågt brus förväntas.

Slutsats

Även om det ibland verkar som om världen har blivit helt digital, visar exemplen som tas upp i denna artikel att den analoga integratorn förblir ett extremt användbart och mångsidigt kretselement för signalbehandling, sensorkonditionering, signalgenerering och filtrering.